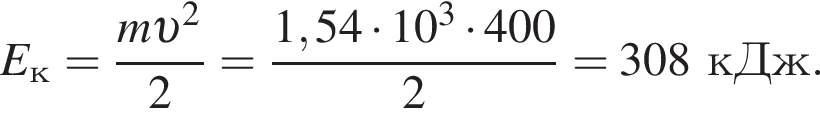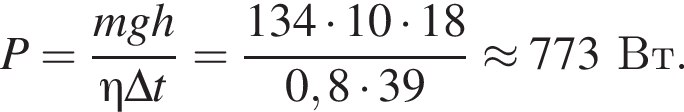Тело двигалось вдоль оси Ох под действием силы
![]() График зависимости проекции силы Fx на ось Ох от координаты х тела представлен на рисунке. На участках (О; а), (а; b), (b; c) сила совершила работу А0а, Ааb, Аbс соответственно. Для этих работ справедливо соотношение:
График зависимости проекции силы Fx на ось Ох от координаты х тела представлен на рисунке. На участках (О; а), (а; b), (b; c) сила совершила работу А0а, Ааb, Аbс соответственно. Для этих работ справедливо соотношение:
Модуль скорости движения υ1 первого тела массой m1 в два раза больше модуля скорости движения υ2 второго тела массой m2. Если кинетические энергии этих тел равны (Ek1 = Ek2), то отношение массы второго тела к массе первого тела равно:
На рисунке изображены три положения груза пружинного маятника, совершающего свободные незатухающие колебания с амплитудой x0. Если в положении В полная механическая энергия маятника W = 8,0 Дж, то в положении Б она равна:
Масса m1 первого тела в два раза больше массы m2 второго тела. Если модули скоростей этих тел равны (υ1 = υ2), то отношение кинетической энергии первого тела к кинетической энергии второго тела ![]() равно:
равно:
На рисунке изображены три положения груза пружинного маятника, совершающего свободные незатухающие колебания с амплитудой x0. Если в положении В полная механическая энергия маятника W = 4,0 Дж, то в положении Б она равна:
Абсолютное удлинение ![]() первой пружины в два раза больше абсолютного удлинения
первой пружины в два раза больше абсолютного удлинения ![]() второй пружины. Если потенциальные энергии упругой деформации этих пружин равны (EП1 = EП2), то отношение жесткости второй пружины к жесткости первой пружины
второй пружины. Если потенциальные энергии упругой деформации этих пружин равны (EП1 = EП2), то отношение жесткости второй пружины к жесткости первой пружины ![]() равно:
равно:
На рисунке изображен математический маятник, совершающего свободные незатухающие колебания между точками А и В. Если в положении А полная механическая энергия маятника W = 12,0 Дж, то в положении Б она равна:
С некоторой высоты h в горизонтальном направлении бросили камень, траектория полёта которого показана штриховой линией (см. рис.). Если в точке Б полная механическая энергия камня W = 12,0 Дж, то в точке А после броска она равна:
Масса m1 первого тела в два раза больше массы m2 второго тела. Если кинетические энергии этих тел равны 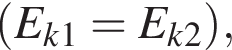 то отношение модуля скорости второго тела к модулю скорости первого тела
то отношение модуля скорости второго тела к модулю скорости первого тела ![]() равно:
равно:
С некоторой высоты h в горизонтальном направлении бросили камень, траектория полёта которого показана штриховой линией (см. рис.). Если в точке Б полная механическая энергия камня W = 8,0 Дж, то в точке А после броска она равна:
Модуль скорости υ1 первого тела в два раза больше модуля скорости движения υ2 второго тела. Если массы этих тел равны 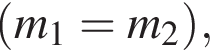 то отношение кинетической энергии первого тела к кинетической энергии второго тела
то отношение кинетической энергии первого тела к кинетической энергии второго тела ![]() равно:
равно:
На рисунке сплошной линией показан график зависимости полной механической энергии Eполн тела от времени t, штриховой линией — график зависимости потенциальной энергии Eп тела от времени t. Кинетическая энергия Eк тела оставалась неизменной в течение промежутка времени:
На рисунке сплошной линией показан график зависимости кинетической энергии Eк тела от времени t, штриховой линией — график зависимости потенциальной энергии Eп тела от времени t. Полная механическая энергия Eполн тела оставалась неизменной в течение промежутка времени:
Материальная точка массой m = 2,0 кг движется вдоль оси Ох. Если кинематический закон движения материальной точки имеет вид 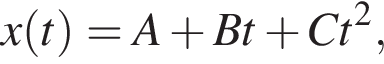 где A = 2,0 м,
где A = 2,0 м, 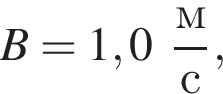
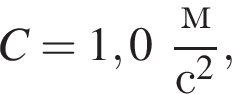 то кинетическая энергия Eк материальной точки в момент времени t = 3,0 с равна ... Дж.
то кинетическая энергия Eк материальной точки в момент времени t = 3,0 с равна ... Дж.
Материальная точка массой m = 2,0 кг движется вдоль оси Ох. Если кинематический закон движения материальной точки имеет вид 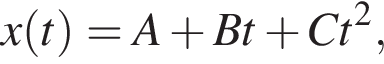 где A = 2,0 м,
где A = 2,0 м, 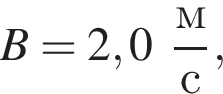
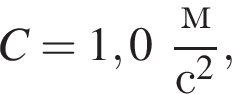 то кинетическая энергия Eк материальной точки в момент времени t = 2,0 с равна ... Дж.
то кинетическая энергия Eк материальной точки в момент времени t = 2,0 с равна ... Дж.
Тело массой m = 0,25 кг свободно падает без начальной скорости с высоты H. Если на высоте h = 20 м кинетическая энергия тела Eк = 30 Дж, то первоначальная высота H равна ... м.
Тело свободно падает без начальной скорости с высоты H = 30 м. Если на высоте h = 20 м потенциальная энергия тела по сравнению с первоначальной уменьшилась на ![]() = 3,0 Дж, то его масса m равна ... г.
= 3,0 Дж, то его масса m равна ... г.
Тело массой m = 0,25 кг свободно падает без начальной скорости с высоты H. Если на высоте h = 20 м потенциальная энергия тела по сравнению с первоначальной уменьшилась на ![]() = 65 Дж, то высота H равна ... м.
= 65 Дж, то высота H равна ... м.
Тело массой m = 0,25 кг свободно падает без начальной скорости с высоты H = 30 м. Тело обладает кинетической энергией ![]() = 30 Дж на высоте h, равной ... м.
= 30 Дж на высоте h, равной ... м.
Камень бросили вертикально вверх с поверхности Земли со скоростью, модуль которой 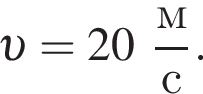 Кинетическая энергия камня равна его потенциальной на высоте h, равной ... м.
Кинетическая энергия камня равна его потенциальной на высоте h, равной ... м.
Тело свободно падает без начальной скорости с высоты h = 17 м над поверхностью Земли. Если на высоте h1 = 2,0 м кинетическая энергия тела Eк = 1,8 Дж, то масса m тела равна ... г.
Тело массой m = 100 г свободно падает без начальной скорости с высоты h над поверхностью Земли. Если на высоте h1 = 6,0 м кинетическая энергия тела Eк = 12 Дж, то высота h равна ... м.
Тело свободно падает без начальной скорости с высоты h = 20 м над поверхностью Земли. Если масса тела m = 200 г, то на высоте h1 = 8,0 м кинетическая энергия Eк тела равна ... Дж.
На рисунке приведён график зависимости кинетической энергии Ек тела, движущегося вдоль оси Ох, от координаты х. На участке АВ модуль результирующей сил, приложенных к телу, равен ... Н.
На гладкой горизонтальной поверхности установлен штатив массой М = 800 г, к которому на длинной нерастяжимой нити подвешен шарик массой m = 200 г, находящийся в состоянии равновесия (см. рис.). Штативу ударом сообщили горизонтальную скорость, модуль которой
На гладкой горизонтальной поверхности установлен штатив массой М = 900 г, к которому на длинной нерастяжимой нити подвешен шарик массой m = 100 г, находящийся в состоянии равновесия (см. рис.). Штативу ударом сообщили горизонтальную скорость, модуль которой
Два маленьких шарика массами m1 = 16 г и m2 = 8 г подвешены на невесомых нерастяжимых нитях одинаковой длины l так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись, hmax = 6,0 см, то длина l нити равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись, hmax = 6,0 см, то длина l нити равна … см.
Два маленьких шарика массами m1 = 24 г и m2 = 12 г подвешены на невесомых нерастяжимых нитях одинаковой длины l = 63 см так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота hmax, на которую они поднялись, равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота hmax, на которую они поднялись, равна … см.
На невесомой нерастяжимой нити длиной l = 98 см висит небольшой шар массой М = 38,6 г. Пуля массой m = 1,4 г, летящая горизонтально со скоростью ![]() попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
Два маленьких шарика массами m1 = 18 г и m2 = 9,0 г подвешены на невесомых нерастяжимых нитях одинаковой длины l так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись hmax = 8,0 см, то длина l нити равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись hmax = 8,0 см, то длина l нити равна … см.
Два маленьких шарика массами m1 = 32 г и m2 = 16 г подвешены на невесомых нерастяжимых нитях одинаковой длины l = 99 см так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое, то максимальная высота hmax на которую они поднялись равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое, то максимальная высота hmax на которую они поднялись равна … см.
Два маленьких шарика массами m1 = 30 г и m2 = 15 г подвешены на невесомых нерастяжимых нитях одинаковой длины l так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись hmax = 10,0 см, то длина l нити равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись hmax = 10,0 см, то длина l нити равна … см.
На невесомой нерастяжимой нити длиной l = 72 см висит небольшой шар массой М = 43,6 г. Пуля массой m = 2,4 г, летящая горизонтально со скоростью ![]() попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
На невесомой нерастяжимой нити длиной l = 1,28 м висит небольшой шар массой М = 58 г. Пуля массой m = 4 г, летящая горизонтально со скоростью ![]() попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
На невесомой нерастяжимой нити длиной l = 72 см висит небольшой шар массой М = 52 г. Пуля массой m = 8 г, летящая горизонтально со скоростью ![]() попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
На невесомой нерастяжимой нити длиной l = 72 см висит небольшой шар массой М = 34 г. Пуля массой m = 3 г, летящая горизонтально со скоростью ![]() попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
Груз массой m = 0,80 кг, подвешенный на длинной невесомой нерастяжимой нити, отклонили так, что нить заняла горизонтальное положение, и отпустили без начальной скорости. В момент времени, когда нить составляла угол α = 60° с вертикалью, модуль силы Fн натяжения нити был равен ... Н.
Груз массой m = 9,0 кг равномерно поднимают с помощью подвижного блока (см. рис.). Если коэффициент полезного действия блока η = 75%, то модуль силы F, приложенной к свободному концу верёвки, равен ... Н.
Груз массой m = 7,2 кг равномерно поднимают с помощью подвижного блока (см. рис.). Если коэффициент полезного действия блока η = 80 %, то модуль силы F, приложенной к свободному концу верёвки, равен ... Н.
Воздух считается загрязнённым диоксидом серы, если в одном кубическом метре воздуха содержится больше чем N0 = 1,9 · 1018 молекул диоксида серы. В одном килограмме диоксида серы находится N1 = 9,4 · 1024. Если в воздух попадёт m = 10 кг диоксида серы, то максимальный объём V загрязнённого воздуха будет равен:
Электроскутер массой m = 130 кг (вместе с водителем) поднимается по дороге с углом наклона к горизонту α = 30° с постоянной скоростью ![]() Сила сопротивления движению электроскутера прямо пропорциональна его скорости:
Сила сопротивления движению электроскутера прямо пропорциональна его скорости: 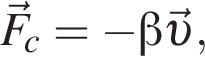 где
где 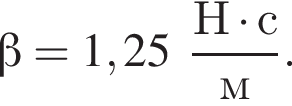 Напряжение на двигателе электроскутера U = 480 В, сила тока в обмотке двигателя I = 40 А. Если коэффициент полезного действия двигателя η = 85%, то модуль скорости υ движения электроскутера равен ...
Напряжение на двигателе электроскутера U = 480 В, сила тока в обмотке двигателя I = 40 А. Если коэффициент полезного действия двигателя η = 85%, то модуль скорости υ движения электроскутера равен ... ![]()
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 70 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0|=200 пКл) шарик массой m = 630 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 80 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 500 пКл) шарик массой m = 380 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 250 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 250 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 20 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0|=400\ пКл) шарик массой m = 180 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 200 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 200 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 38 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 400 пКл) шарик массой m = 100 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 100 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 100 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 40 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 100 пКл) шарик массой m = 720 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 10 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 100 пКл) шарик массой m = 380 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 100 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 100 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Подъёмный кран равномерно поднимает железобетонную плиту массой m = 3,0 т на высоту h = 21 м за промежуток времени Δt = 1,0 мин. Если коэффициент полезного действия подъёмного крана η = 80%, то мощность P, развиваемая электродвигателем крана,
Невесомая пружина жёсткостью
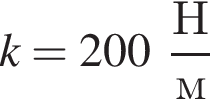 закреплена вертикально на столе. К верхнему концу пружины прикреплена лёгкая горизонтальная пластинка. С высоты h = 25 см (см. рис.) на пластинку без начальной скорости падает маленький шарик массой m = 190 г и прилипает к ней. Если длина пружины в недеформированном состоянии l0 = 30 см, то в ходе колебаний пластинка с шариком будет подниматься относительно поверхности стола на максимальную высоту H, равную ... см.
закреплена вертикально на столе. К верхнему концу пружины прикреплена лёгкая горизонтальная пластинка. С высоты h = 25 см (см. рис.) на пластинку без начальной скорости падает маленький шарик массой m = 190 г и прилипает к ней. Если длина пружины в недеформированном состоянии l0 = 30 см, то в ходе колебаний пластинка с шариком будет подниматься относительно поверхности стола на максимальную высоту H, равную ... см.
Ответ запишите в сантиметрах, округлив до целых.
Подъёмный кран равномерно поднимает железобетонную плиту массой m = 2,5 т на высоту h = 16 м за промежуток времени Δt = 1,5 мин. Если мощность, развиваемая электродвигателем крана, P = 6,0 кВт, то коэффициент полезного действия η подъёмного крана
Невесомая пружина жёсткостью k = 200 Н/м закреплена вертикально на столе. К верхнему концу пружины прикреплена лёгкая горизонтальная пластинка. С высоты h = 30 см (см. рис.) на пластинку без начальной скорости падает маленький шарик массой m = 150 г и прилипает к ней. Если длина пружины в недеформированном состоянии l0 = 35 см, то в ходе колебаний пластинка с шариком будет подниматься относительно поверхности стола на максимальную высоту H,
Ответ запишите в сантиметрах, округлив до целых.
Небольшое тело скользит по гладкой поверхности горки в вертикальной плоскости. Зависимость высоты h точек поверхности горки от координаты x показана на рисунке. Нулевой уровень потенциальной энергии совпадает с горизонтальной осью Ох. Если в точке A потенциальная энергия тела была в два раза больше его кинетической энергии, то точки, в которые тело не может переместиться из точки A, обозначены цифрами:
Автомобиль трогается с места и, двигаясь равноускорено и прямолинейно, проходит по горизонтальному участку шоссе путь s = 20,0 м за промежуток времени Δt = 2,00 с. Если масса автомобиля m = 1,00 т, то его кинетическая энергия Ek в конце пути
Плита массой m = 120 кг была равномерно поднята с помощью подъемного механизма на высоту h = 16,0 м за промежуток времени Δt = 30,0 c. Если коэффициент полезного действия 80%. то мощность, развиваемая двигателем, равна ... Вт.
Небольшое тело скользит по гладкой поверхности горки в вертикальной плоскости. Зависимость высоты h точек поверхности горки от координаты x показана на рисунке. Нулевой уровень потенциальной энергии совпадает с горизонтальной осью Ox. Если в точке A потенциальная энергия тела была в два раза меньше его кинетической энергии, то точки, в которые тело не может переместиться из точки A, обозначены цифрами:
Автомобиль трогается с места и, двигаясь равноускорено и прямолинейно, проходит по горизонтальному участку шоссе путь s = 20,0 м за промежуток времени Δt = 2,00 c. Если масса автомобиля m = 1,54 т, то его кинетическая энергия Eк в конце пути
Плита массой m = 134 кг была равномерно поднята с помощью подъёмного механизма на высоту h = 18,0 м за промежуток времени Δt = 39,0 с. Если коэффициент полезного действия подъёмного механизма η = 80,0 %, то мощность P, развиваемая электродвигателем механизма,

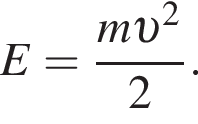 По условию
По условию 
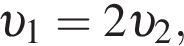 значит,
значит,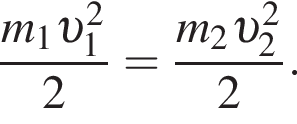
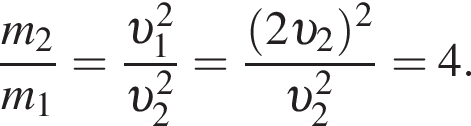

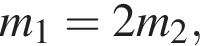 значит,
значит,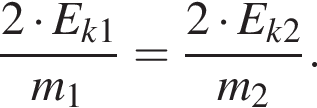
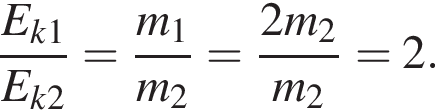
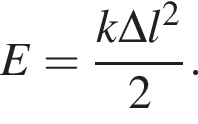 По условию
По условию 
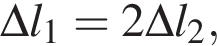 значит
значит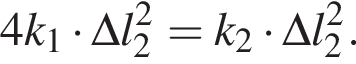
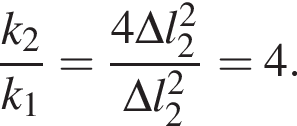

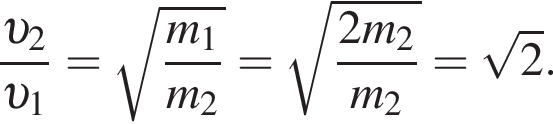
 значит
значит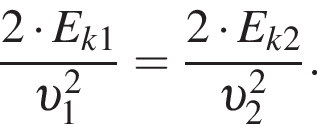
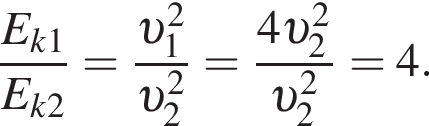
 то кинетическая энергия не изменялась на промежутке времени от 0 до 1 с, когда графики полной механической энергии и потенциальной энергии тела были параллельными.
то кинетическая энергия не изменялась на промежутке времени от 0 до 1 с, когда графики полной механической энергии и потенциальной энергии тела были параллельными. то полная энергия не изменялась на промежутке времени от 2 до 3 с, когда эта сумма равнялась 7 Дж.
то полная энергия не изменялась на промежутке времени от 2 до 3 с, когда эта сумма равнялась 7 Дж.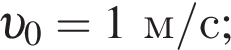
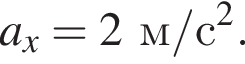 Скорость материальной точки при равноускоренном движении равна
Скорость материальной точки при равноускоренном движении равна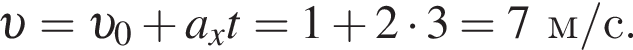
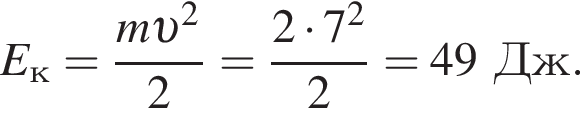
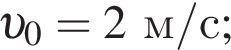
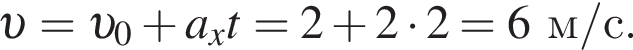
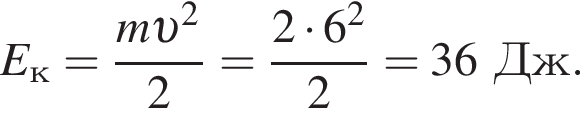
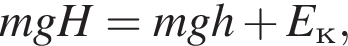 следовательно,
следовательно, 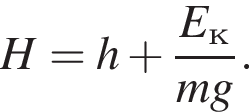
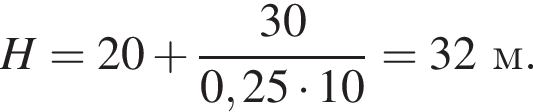
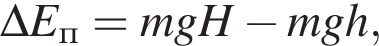 следовательно,
следовательно,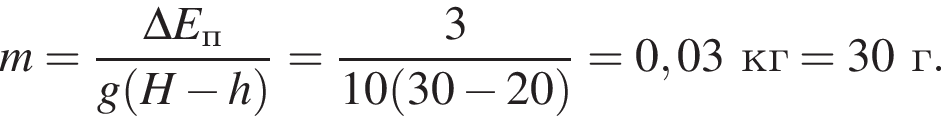
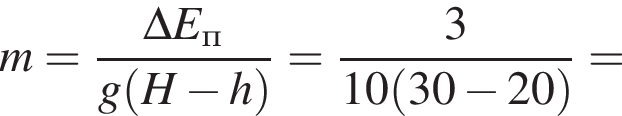

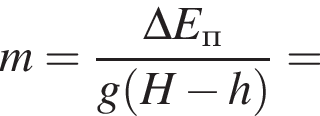
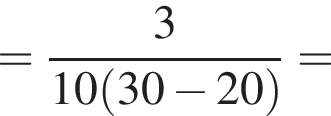
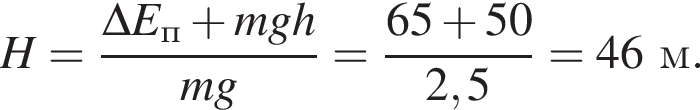
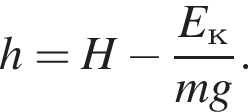
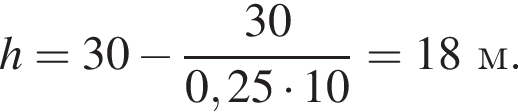
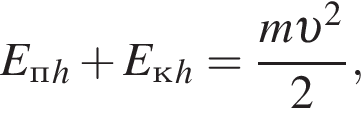 где Eпh − потенциальная энергия на высоте h, Eкh − кинетическая энергия на высоте h, они равны, значит,
где Eпh − потенциальная энергия на высоте h, Eкh − кинетическая энергия на высоте h, они равны, значит, 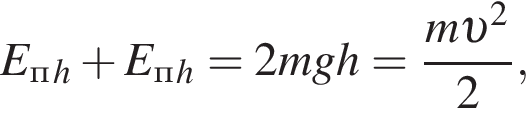 следовательно,
следовательно,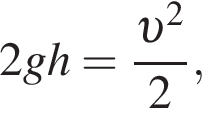
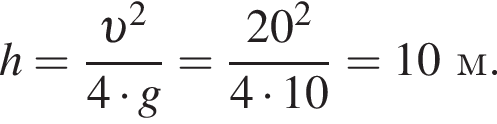
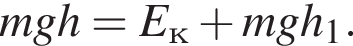
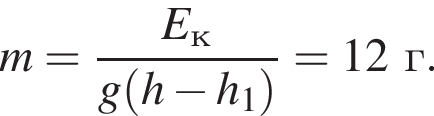
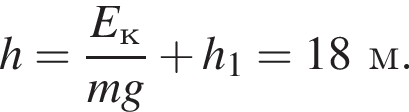
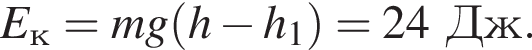
 С другой стороны работа равна A = Fx · sx, где проекция перемещения равна sx = x2 − x1. Отсюда проекция равнодействующей силы равняется
С другой стороны работа равна A = Fx · sx, где проекция перемещения равна sx = x2 − x1. Отсюда проекция равнодействующей силы равняется 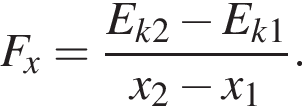
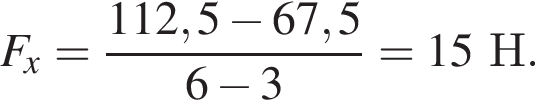 Тогда модуль равнодействующей силы равен 15 Н.
Тогда модуль равнодействующей силы равен 15 Н.
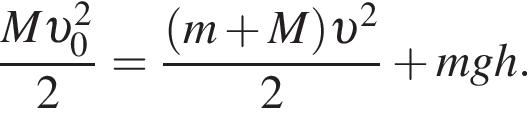
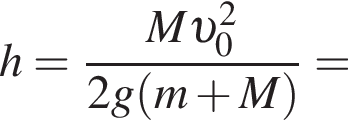
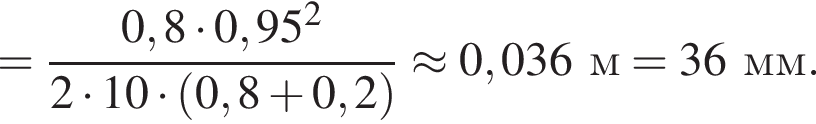
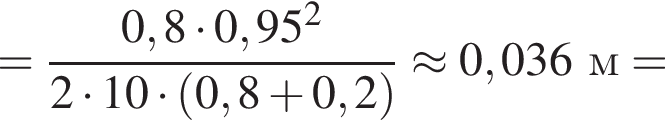
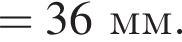

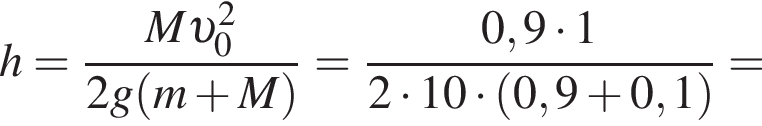
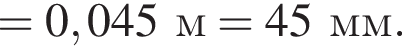
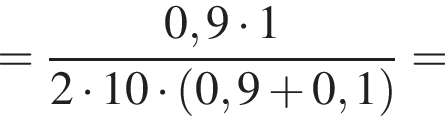
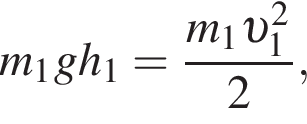
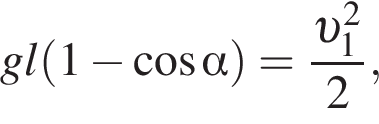
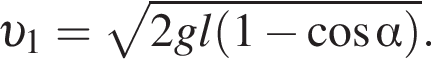

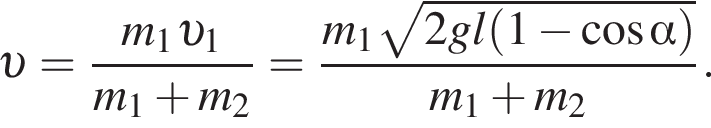
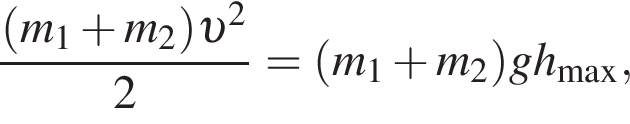
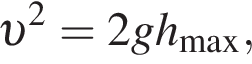
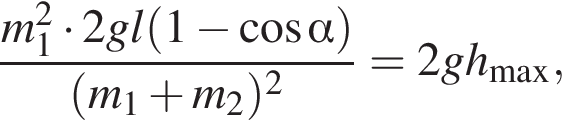
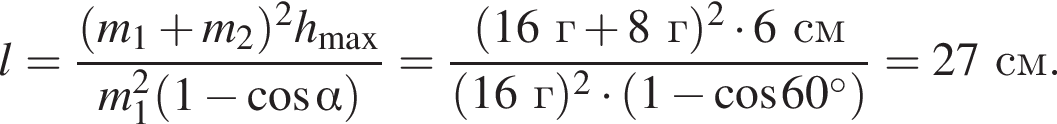
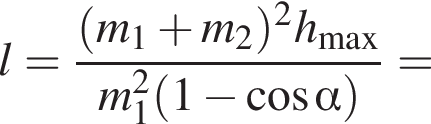
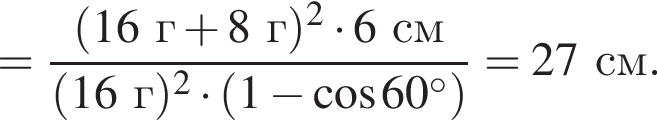
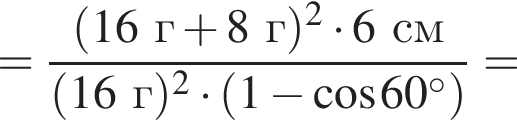
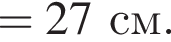
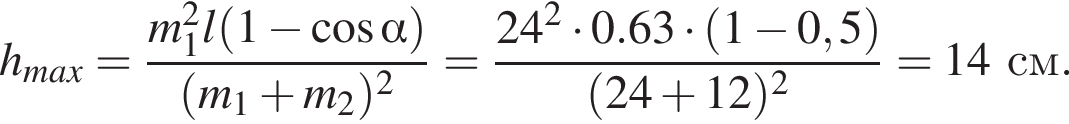
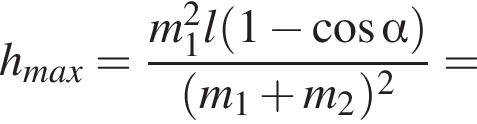
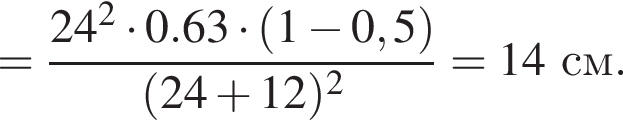
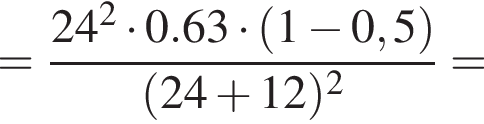
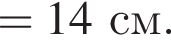
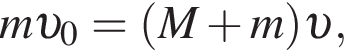
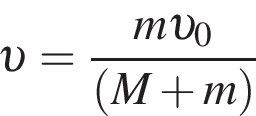 — скорость системы "пуля+шар" после застревания пули.
— скорость системы "пуля+шар" после застревания пули.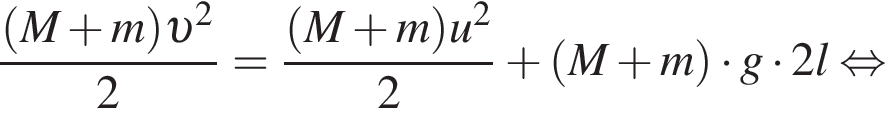
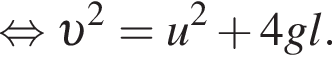
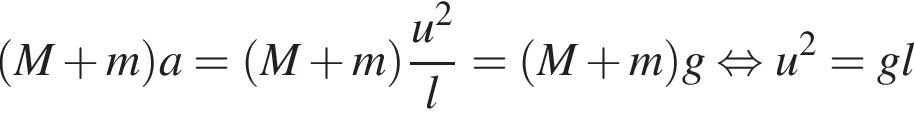
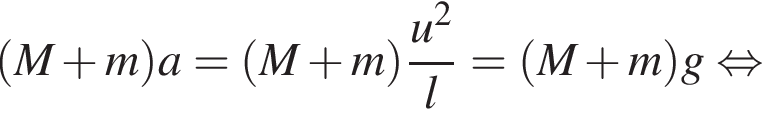
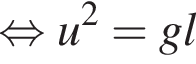
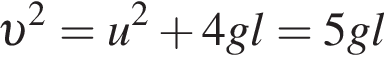
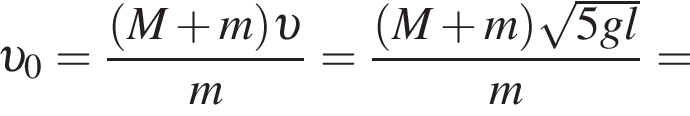
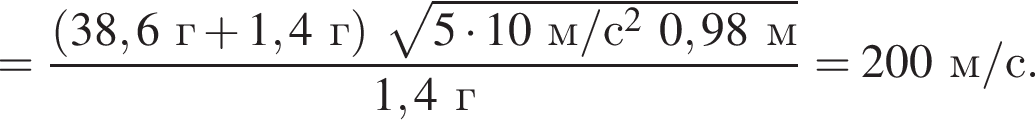
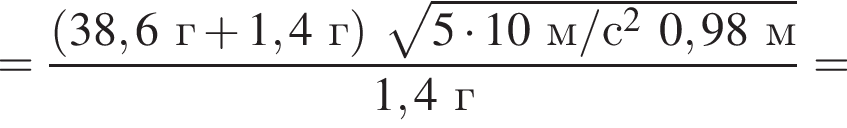
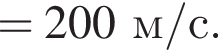
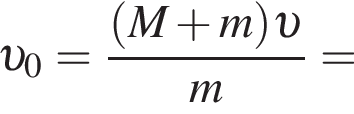
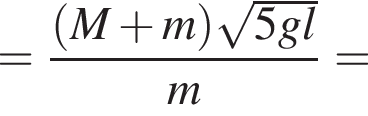
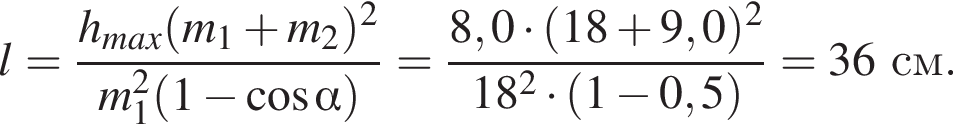
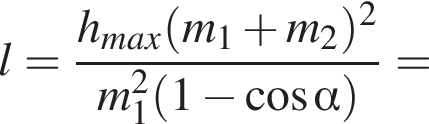
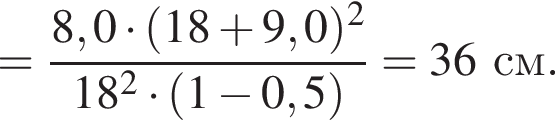
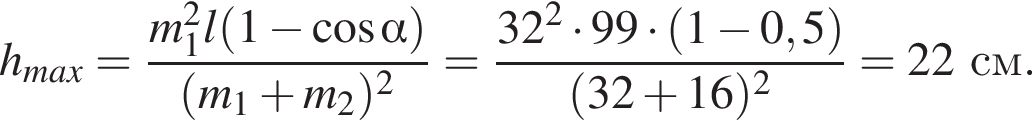
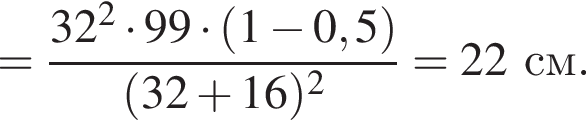
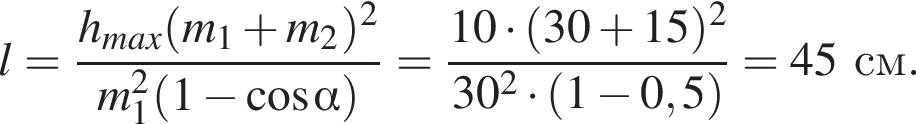
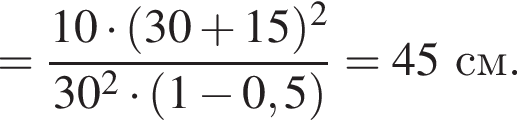

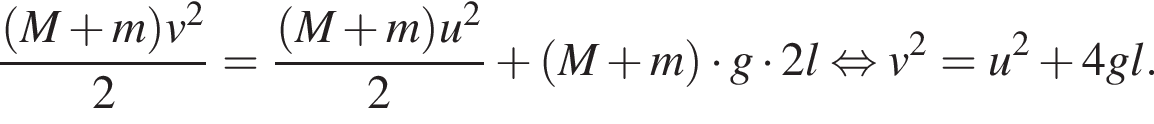
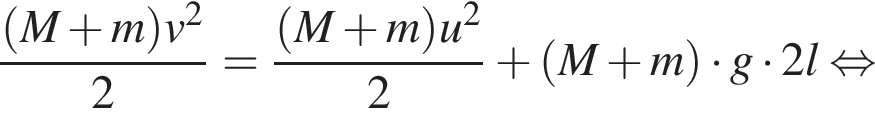
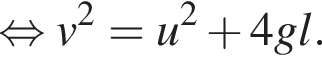
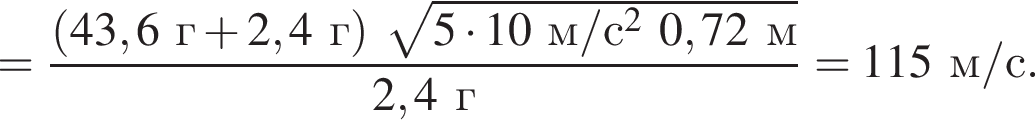
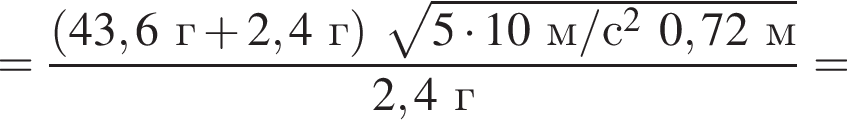
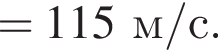
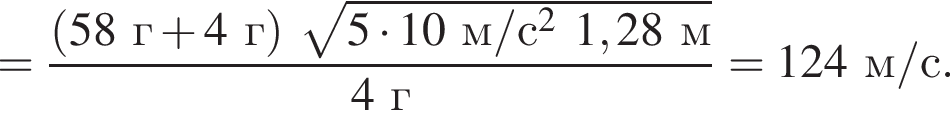
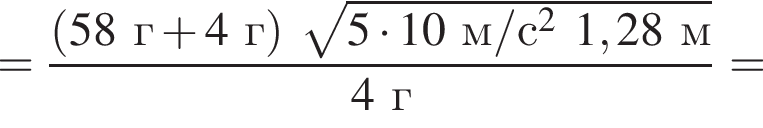
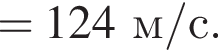
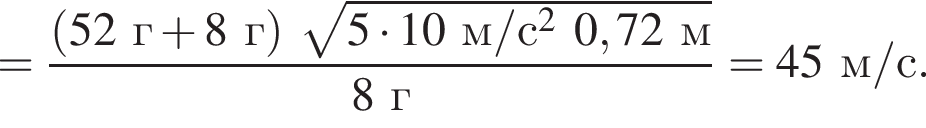
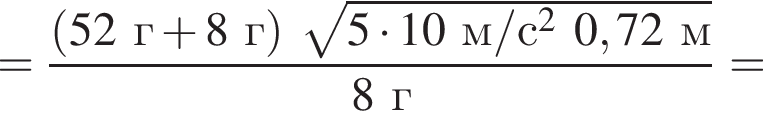
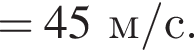
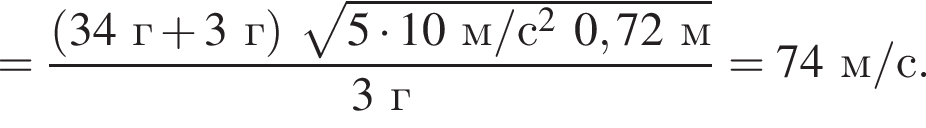
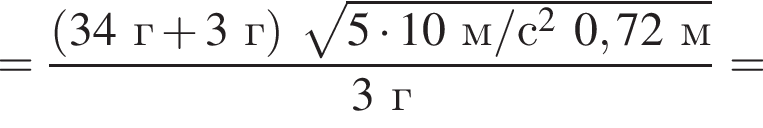
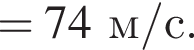
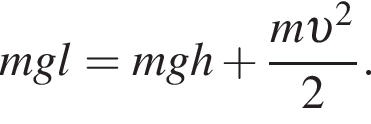
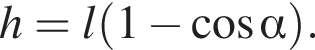 Тогда имеем:
Тогда имеем: 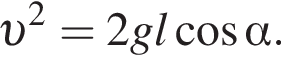
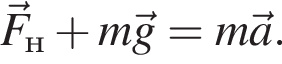 При проецировании на ось, совпадающую с направлением ускорения получаем:
При проецировании на ось, совпадающую с направлением ускорения получаем:
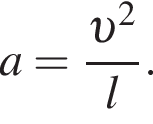
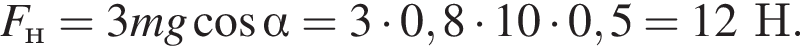
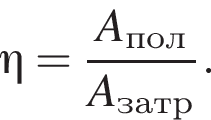 При этом полезная работа
При этом полезная работа  затраченная работа
затраченная работа  Объединяя формулы, находим модуль силы, приложенной к свободному концу веревки
Объединяя формулы, находим модуль силы, приложенной к свободному концу веревки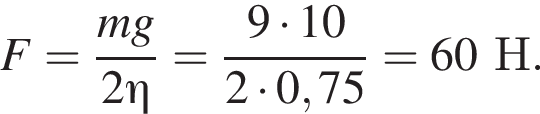
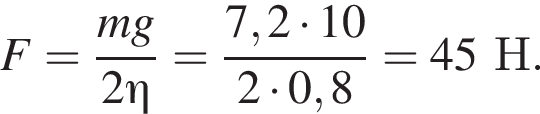
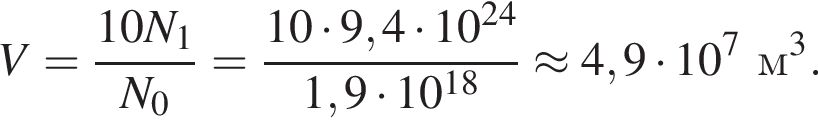
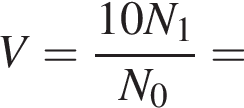
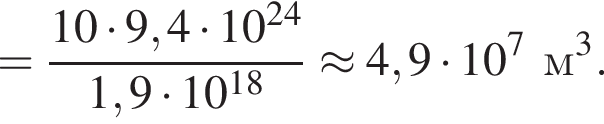
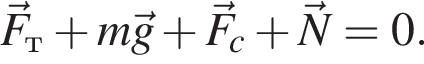


 затраченная мощность
затраченная мощность 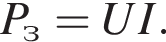
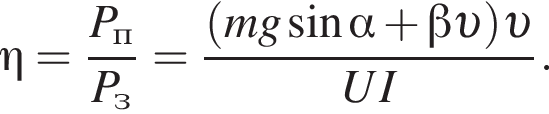
 решением которого будет
решением которого будет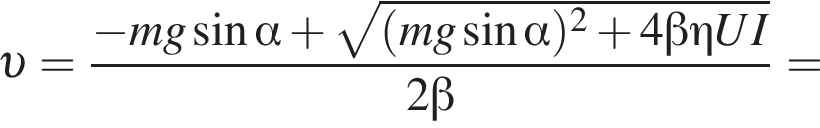
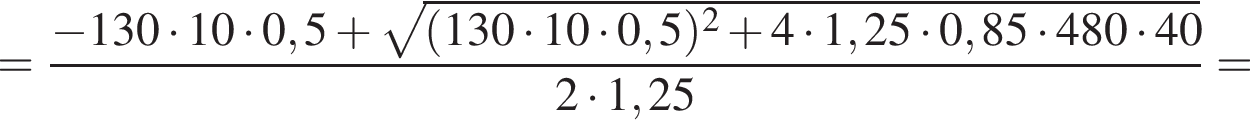
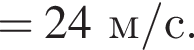
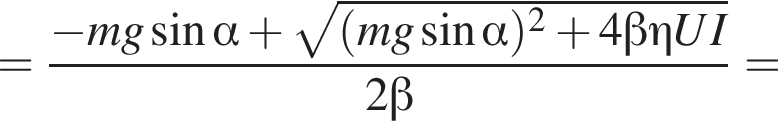
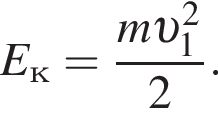 В электрическом поле шарик разгоняется, увеличивая свою кинетическую энергию на
В электрическом поле шарик разгоняется, увеличивая свою кинетическую энергию на  В установившемся режиме после соударения с противоположной пластиной кинетическая энергия шарика уменьшается до исходного значения
В установившемся режиме после соударения с противоположной пластиной кинетическая энергия шарика уменьшается до исходного значения 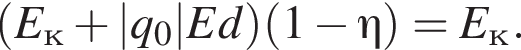
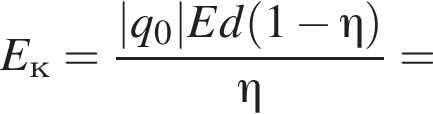
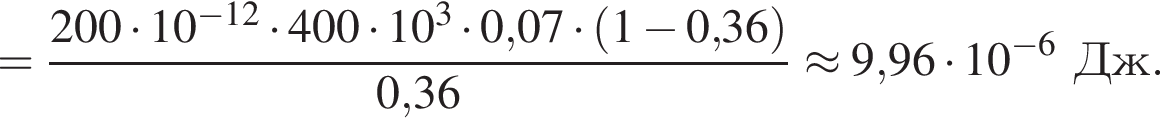
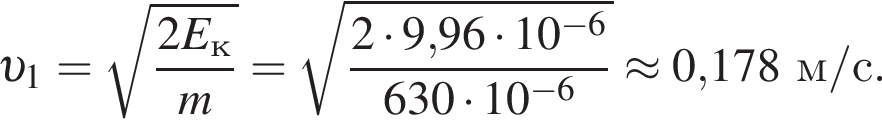
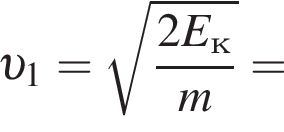
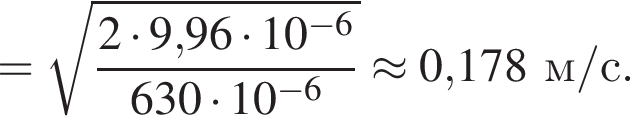
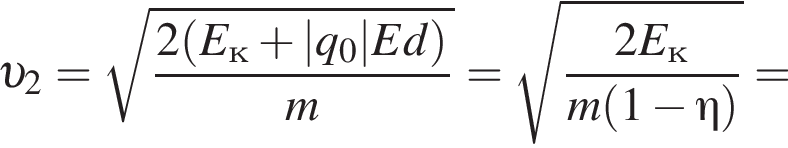
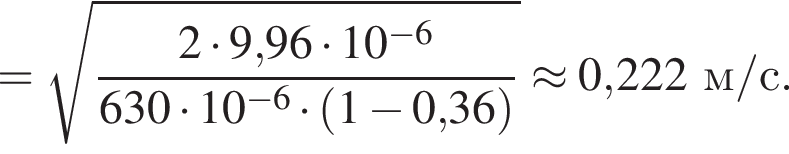
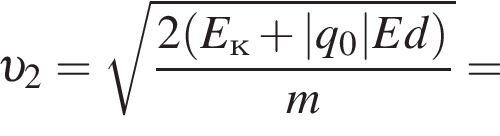
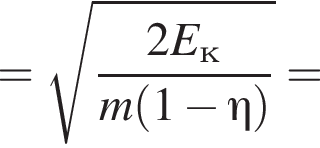
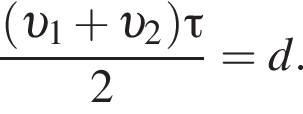
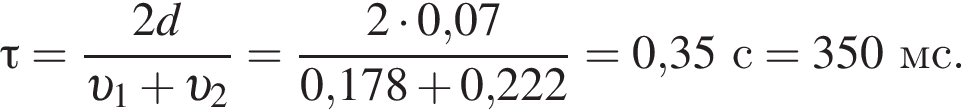
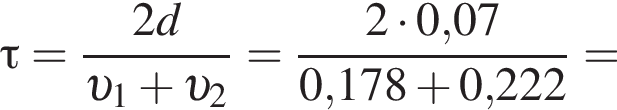
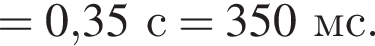
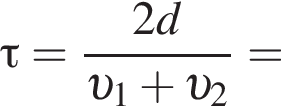
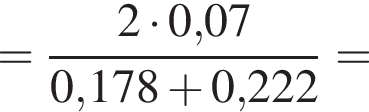

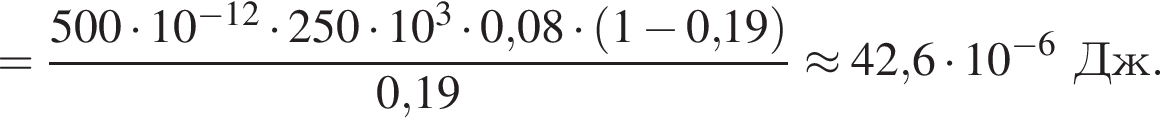
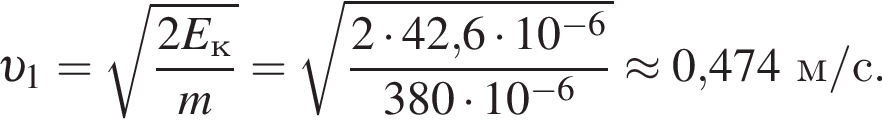
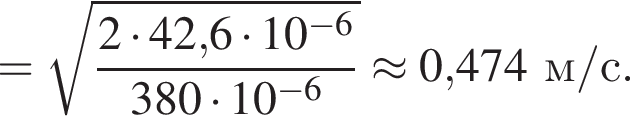
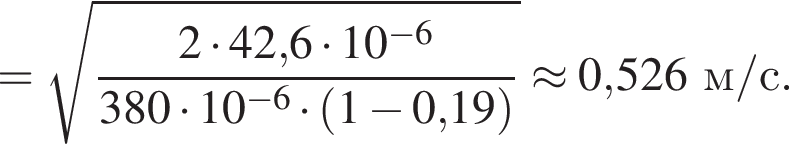
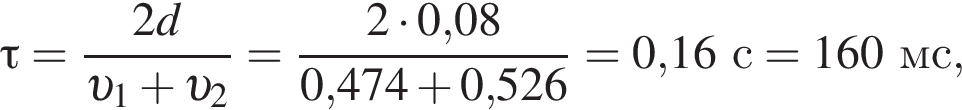
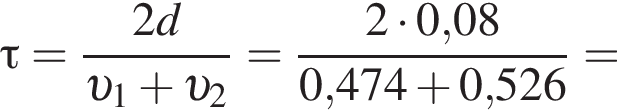
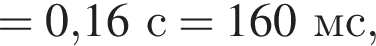
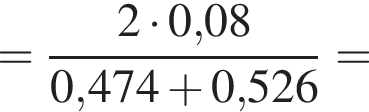

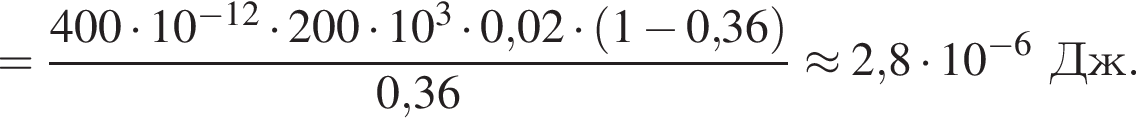
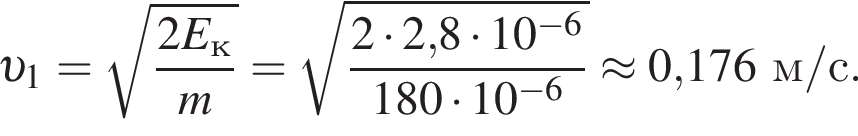
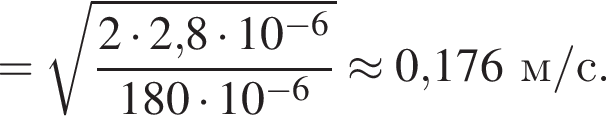
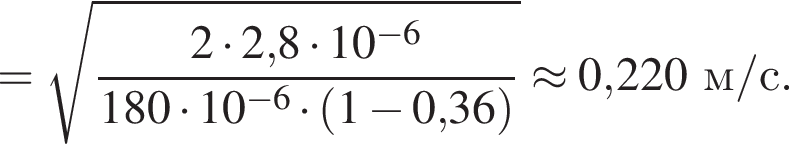
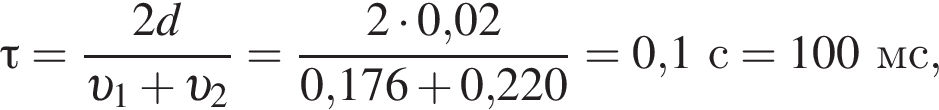
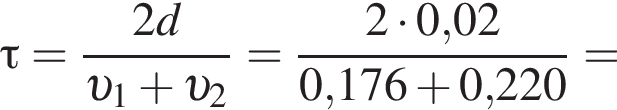

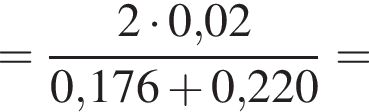

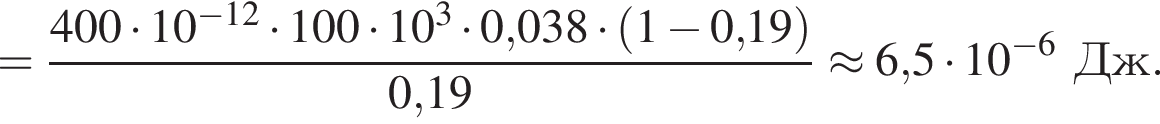
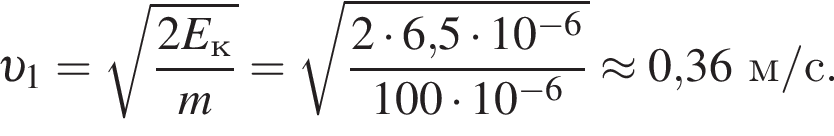
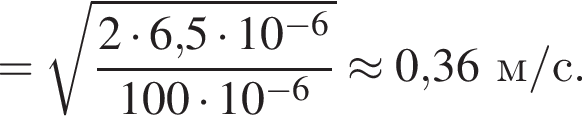
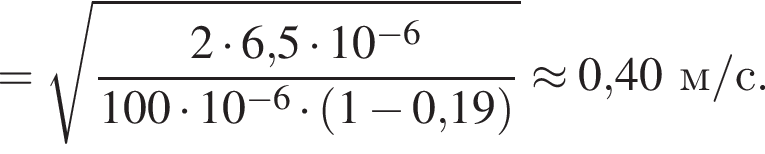
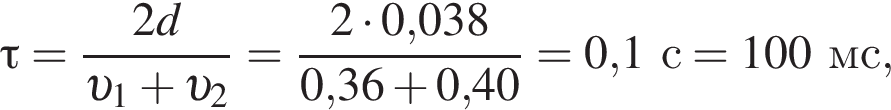
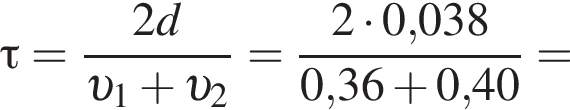
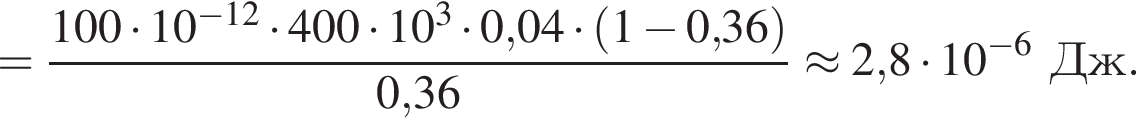
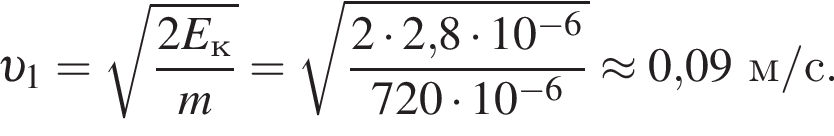
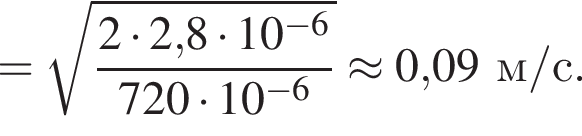
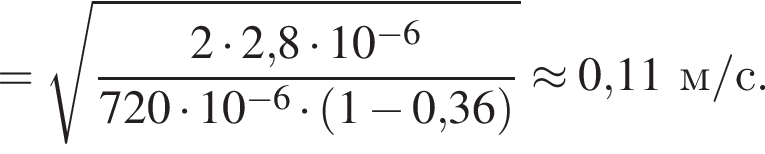
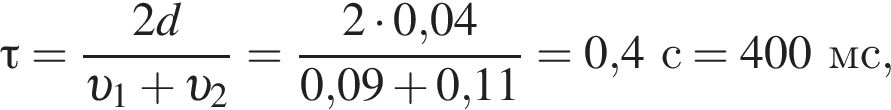
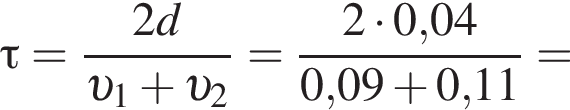


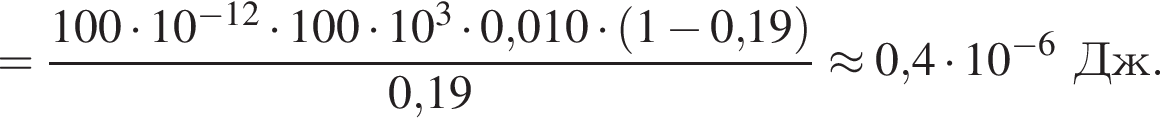
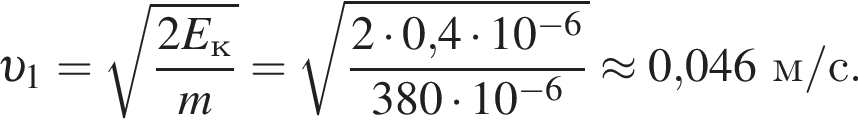
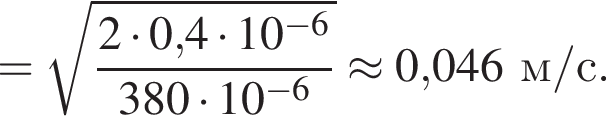
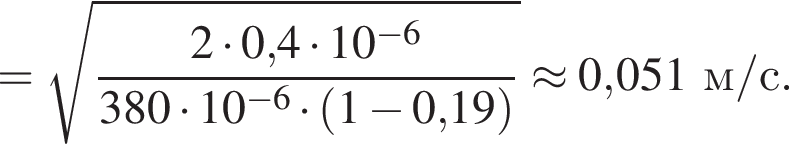
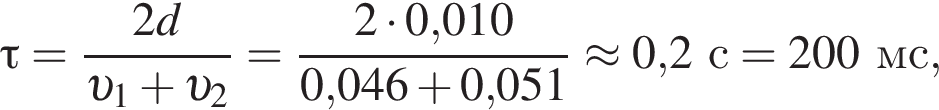
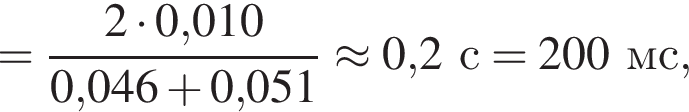
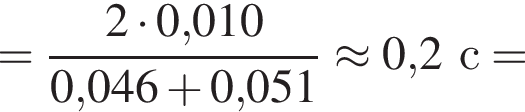
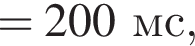

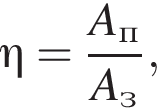 где полезная работа
где полезная работа  затраченная работа
затраченная работа 
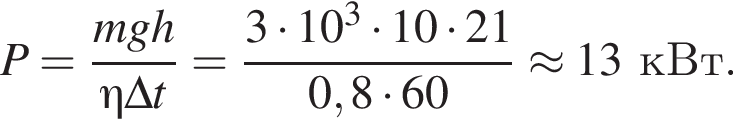
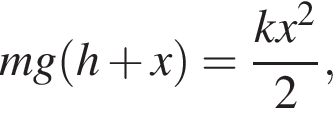
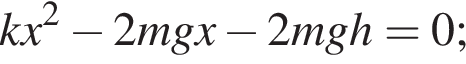
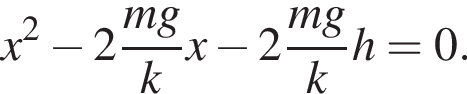
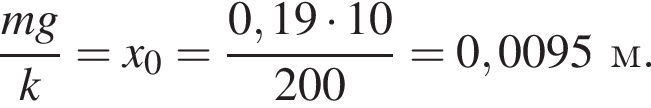
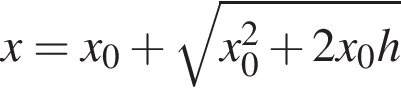
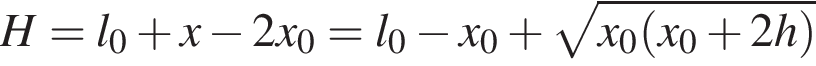
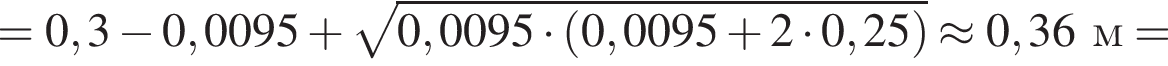
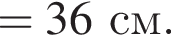
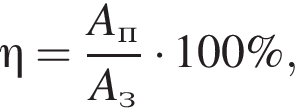 где полезная работа
где полезная работа 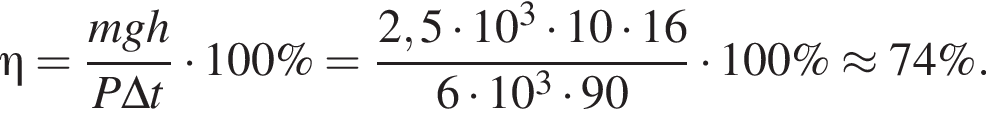
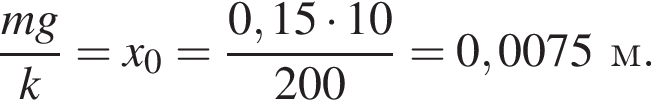
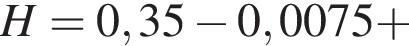


 что больше полной энергии тела. Следовательно, в данную точку тело подняться не сможет. Значит, в точку 1 тело не попадет.
что больше полной энергии тела. Следовательно, в данную точку тело подняться не сможет. Значит, в точку 1 тело не попадет.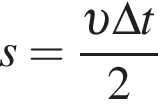 найдем его скорость в конце пути:
найдем его скорость в конце пути: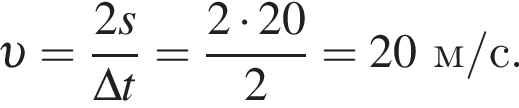

 где полезная работа по равномерному подъему груза
где полезная работа по равномерному подъему груза 


 что больше полной энергии тела. Следовательно, в данную точку тело подняться не сможет. Значит, в точки 4 и 5 тело не попадет.
что больше полной энергии тела. Следовательно, в данную точку тело подняться не сможет. Значит, в точки 4 и 5 тело не попадет.